Project Objectives

The new frontier of Content Based Information Systems is the so called ``Semantic Web'' (see others/w3c_bl98). Associating meaning with content or establishing a layer of machine understandable data will allow automated agents, sophisticated search engines and interoperable services and will enable higher degree of automation and more intelligent applications. The ultimate goal of the Semantic Web is to allow machines to share and exploit knowledge in the Web way, i.e. without central authority, with few basic rules, in a scalable, adaptable, extensible manner. However, the actual development of the Semantic Web and its technologies has been hindered so far by the lack of large scale, distributed repositories of structured, content oriented information. The case of Mathematical knowledge, the most rigorous and condensed form of knowledge, is paradigmatic. The World Wide Web is already now the largest single resource of mathematical knowledge, and its importance will be exponentiated by the emerging display technologies like MathML. However, almost all mathematical documents available on the Web are marked up only for presentation (in this respect, current practice in MathML improves on, but does not fundamentally differ from the older paper-oriented markup schemes like LaTeX or Postscript). A consequence of this is that the online material is machine-readable, but not machine-understandable, severely crippling the possibility to offer added-value services like

Preservation of the real informative content in a highly structured and machine understandable format, suitable for transformation, automatic elaboration and processing.
Cut and paste on the level of computation (take the output from a Web search engine and paste it into a computer algebra system).
Automatic proof checking of published proofs.
Semantical search for mathematical concepts (rather than keywords).
Classification: given a concrete mathematical structure, is there a general theory for it?

Due to its rich notational, logical and semantical structure, mathematical knowledge is thus a main case study for the development of the new generation of semantic Web systems. The aim of the proposed project is both to help in this process, as well as pave the way towards a really useful virtual, distributed, hyper-textual resource for the working mathematician, scientist or engineer. All modern sciences have a strongly mathematicised core, and will benefit. The real market and application area for the techniques developed in this project, apart from the obvious realm of education, lies with high-tech and engineering corporations that rely on huge formula databases. Currently, both the content markup as well as the added-value services alluded to above are very underdeveloped, limiting the usefulness of the vital knowledge. The infrastructure and knowhow needed for mining this information treasure and obtaining a competitive edge in development is exactly what we are attempting to develop in our project.

Several languages have been already proposed for the management of mathematical information on the Web, both for publishing, communication and archiving purposes: most notably, MathML, OpenMath, OMDoc. Other languages must be also considered for definition and specification of Metadata, such as the Dublin Core System, or the Resource Description Framework [RDF]. All these languages, which tend to cover different and orthogonal aspects of the management of mathematical documents, must be eventually taken into account for the ambitious goal of our project. One of our aims is actually the definition of a modular architecture which could exploit the distinctive potentialities of each one of these languages, integrating them into a single application. The integration is in this case facilitated by the fact that all the languages mentioned are particular instances of XML, providing the opportunity to use standard XML technology, and in particular XSL Transformations or stylesheets [XSLT], to pass from one language to the other.

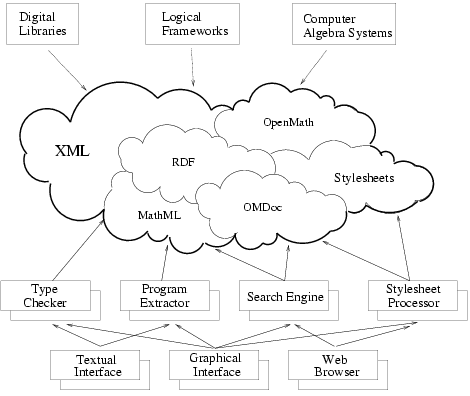
The fact of encoding also the microscopic, logical level of mathematics opens the possibility to have completely formalised subsystems of the library, which could be checked automatically by standard tools for the automation of formal reasoning and the mechanisation of mathematics (proof assistants and logical frameworks, see others/cup_hp91 and others/cup_hp93). At the same time, any of these tools could be used as an authoring system for documents of the library, by simply exporting their internal libraries into XML, and using stylesheets to transform the output into a standard, machine-understandable representation, such as MathML content markup or OpenMath.

The precise formal content can still be preserved by the machinery of Xlinks. Moreover, stylesheets can be also used to solve the annoying notational problem that usually afflicts formal mathematics, providing a simple way for adding user-defined styles and notations.

So, our approach leads to a natural integration of proof assistant tools and the Web. In this integration, the emphasis is just on ``content'': we do not try to link directly the specific applications to the Web, that would be a major mistake, for obvious modularity reasons. On the contrary, we adopt XML as a neutral specification language, and then we merely work on XML-documents, forgetting the underlying application. In this way, similar software tools can be applied to different logical dialects, regardless of their concrete nature. Moreover, if having a common representation layer is not the ultimate solution to all inter-operability problems between different applications, it is however a first and essential step in this direction. Finally, this ``standardisation'' process should naturally lead to a substantial simplification and re-organisation of the current, ``monolithic'' architecture of logical frameworks. All the many different and often loosely connected functionalities of these complex programs (proof checking, editing, search and consulting, program extraction, and so on) could be clearly split in more or less autonomous tasks, and could be developed by different teams, in totally different languages. This is the new, ``content-based'' architectural design of future systems.

Index

This page is hosted by the Department of Computer Science, University of Bologna.
Last updated Fri Feb 2 17:12:17 CET 2007.